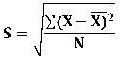CALCULO DE LA MEDIA, MEDIANAY MODA (DATOS NO AGRUPADOS).

Calcular e interpretar las medidas de tendencia central.
Un estudio sobre ausentismo de los obreros de la fábrica A en cierto mes del año, condujo a la tabla siguiente:

No. De días	Total
0	17
1	25
2	15
3	7
4	4
5	2
6	2

Solución: se trata de la variable “No. de ausencias” es de tipo cardenal y de asignaremos la letra Z= a numero de ausencias en días.

z	f	dfa(+)	fz
0	17	17	0
1	25	42	25
2	15	57	30
3	7	64	21
4	4	68	16
5	2	70	10
6	2	72	12

Interpretación: durante el mes considerando, los obreros faltaron a sus labores 1.58 días.

MEDIANA

Interpretación: por lo menos la mitad de los obreros se ausentaron 1 día a sus labores durante el mes.

MODA

Interpretación: el caso más notorio es el de los obreros que dejaron de trabajar un día en el mes. El 34.7% de los obreros tuvieron esa característica.

CALCULO DE LA MEDIANA, MEDIA Y MODA (DATOS AGRUPADOS).

 
 

N: Es el total de datos.

L: Es el límite real inferior.

∑fd: Frecuencia acumulada menor al intervalo

fj: La frecuencia.

j: La anchura real.

Calcular e interpretar la media mediana y moda de la tabla siguiente:

Alumnado según tiempo dedicado al estudio fuera de clases 5ºA 2010

horas

total

1-3	50
4-6	38
7-9	29
10-12	36
13-15	19
16-18	7
19-21	7
22-28	5

datos	f	dfa	puntos medios	fy
1-3	50	50	2	100
4-6	38	88	5	190
7-9	26	114	8	208
10-12	36	150	11	396
13-15	19	169	14	266
16-18	7	176	17	199
19-21	7	183	20	140
22-28	5	188	25	125

 

Interpretar: la mitad del 5º A se dedica al estudio de 1 a 7 horas a la semana.

 

MEDIDAS DE DISPERSIÓN

Una medida de tendencia central por si sola no describe ni resume adecuadamente una distribución de datos; es necesario acompañarla de un indicador que de cuenta del grado o dispersión con que se distribuyen los datos de la variable. Una medida de dispersión dice cuanto se desvían los datos respecto a las tendencias centrales.

RANGO: se trata dela mas simple de las medidas de dispersión. Representa la distancia entre al mayor y el menor de los datos de una distribución por lo cual pueden ser interpretados como la dispersión total de todos ellos. Como es “distancia” se le obtiene restando el dato menor del dato mayor.

El rango, si bien brinda una primera ideal de la dispersión de un conjunto de datos, tiene el inconveniente de que solo toma en cuanta los dos valores extremos y descuida los intermedios; es decir, no dice cuando se desvía un dato intermedio de la tendencia central.

DESVIACION MEDIA: la desviación media fue la medida de dispersión de más uso. Su desplazamiento del arsenal estadístico se debió a la aparición del concepto de desviación estándar.

La desviación media se define como la desviación promedio de los valores absolutos en las desviaciones de los datos de una variable con respecto a su medida. Y se expresa en las unida de la variable (años, horas, peso etc.).

Desviación estándar y varianza (seria de datos simples, sin     frecuencia asociada).

La desviación estándar es la medida de dispersión mas adecuada por sus propiedades algebraicas; se le conoce también como desviación típica. Su símbolo con mayúscula S y se define:

Como la desviación promedio de los datos de una distribución respecto a su medida se puede ver la hallada en casos concretos, debe ser expresada en las mismas unidades. Finalmente para hallar la desviación estándar se extrae la raíz cuadrada y se obtiene la variable.

Hallar e interpretar la varianza y desviación estándar de la variable y cuyos datos son:

6, 7, 7, 7, 8, 9, 10, 11, 12,15

Solución: por razones de claridad y método, conviene preparar 3 columnas para una para los datos otro para deviaciones de datos respecto a su medida y otra mas para las desviaciones cuadráticas.

 

 

Interpretación: los datos de la variable y se separan 2.67 unidades en promedio con respecto a la media.

RANGO:

MEDIDAS DE TENDENCIA CENTRAL: MEDIA, MEDIANA, MODA (SERIE DE DATOS SIMPLES, SIN FRECUENCIAS ASOCIADAS).

Las medidas de tendencia central son categorías o puntos dentro del recorrido de una variable, se les llama de tendencia central porque entorno a ellas parecen agruparse los datos, por ello bien se les puede considerar como sintetizadores. En general, cualquier medida de tendencia es un valor promedio, ya que este, por definición, es todo valor que se halla entre dos extremos.

MEDIA ARITMETICA.

Es la mas conocida de las medidas de tendencia central, aunque no con ese nombre. Se le conoce también con los nombres de valor medio, promedio aritmético o simplemente media. Se les simboliza con cualquiera de las letras, convenidas para representar variables, coronada con una barrita. Se define como la suma de un conjunto de cantidades divididas entre el número de ellas. El símbolo que expresa: 

Donde: X simboliza los datos de una variable y

        N, el número de ellos por ejemplo: si

 

su promedio aritmético es:

MEDIANA

Llamada también valor mediano, es el punto dentro del recorrido de una variable, que supera a no más de la mitad de los datos y esperado por no más de la otra mitad. Dicho de otra manera: es un punto dentro de una distribución de datos que tienen la característica de dividirla en dos partes iguales. La identificaremos por el símbolo de Me.

Tratándose de serie de datos sin frecuencia asociada, no se necesita ninguna formula para hallarla, pero es preciso ordenarlos de menor a mayor o viceversa.

Si el número de datos de la variable es par, la mediana es la semisuma de los dos valores e intermedios que satisfacen su definición.

Me ejemplo: 

*Distribucion par :

MODA

También llamada modo o valor modal es el dato de la variable que tiene mayor frecuencia. Se trata, de hecho, el caso más notorio o típico de una distribución y se simboliza con Mo.

Ejemplo:

Distribución:

EJERCICIOS:

Determina la media, mediana y moda de las distribuciones siguientes:

 

MEDIDAS DE TENDENCIA CENTAL Y DE DISPERCIÓN.

Aprendimos que las masas de los datos no se recopilan en forma de tablas con indicadores pre calculados que las describan y sinteticen; al contrario: Determina una recopilación de datos que parece no tener pies ni cabeza. Su objetivo es obtener de ellos una imagen lo más claro posible; pero por lo general, seria imposible entenderlos e interpretarlos cabalmente si no se dispusiera de algunos indicadores que los resumiera. Estos son dos principalmente: una medida de tendencia central “una especia de promedio” y otra de dispersión, que dice cuanto se separan los datos respecto al promedio.

Antes de empezar el estudio de algunas medidas de tendencia central y de dispersión, nos familiaricemos con la notación que le es propia.

NOTACION SIGMA.

En la inmensa mayoría de los cálculos estadísticos siempre hay un paso que consiste en sumar conjuntos de cantidades. Por esta razón se ha convertido que se utilice un símbolo propio, la letra griega sigma (∑) para indicar que hay que sumar lo que aparece a su derecha. Este símbolo se conoce como sumatoria y se debe de leer: “efectúa la suma de” o, simplemente “la sumatoria de”. También se buscan en mayúsculas la ultimas letras de nuestro abecedario para denotar variables (X, Y, Z, W, etc.) y las primeras letras para constantes (A, B, C, etc.).  

REGLAS DE LA SUMATORIA.

Estudiaremos las reglas fundamentales que gobiernan por decirlo así el uso de la sumatoria.

1. Sumatoria de los datos de una variable.

Para hallar la sumatoria de los datos de una variable, no hay mas procedimientos que el de la agregación, es decir agregar a cada dato el que sigue, hasta terminar. Simbólicamente, esta regla se describe así: 

Ejemplo: numero de hijas por familia 

 

2.-Sumatoria de una constante. 

La sumatoria de una constante que aparece en un conjunto, es simplemente n veces la constante:

Si tenemos cinco valor de C, y si C=10 

La diferencia entre la primera y la segunda es que la primera x es una variable que adopta diversos valores, mientras que la segunda C es un valor que no cambia.
  

3.-Sumatoria de una variable y una constante sumada o restada.   
 La  sumatoria de los datos de una variable y una constante sumada o restada, es igual a la suma de los datos de la variable mas n veces la constante. La expresión: 

Ordena primero sumar la constante C o cada dato dela variable X y después hallar la sumatoria de todos los valores (X+n). Retomando los valores de X y C que nos han servido para simplificar ejemplo:

 

Si reagrupamos sumandos, resulta:

 

El primer término del segundo miembro de la igualdad anterior es ∑X  y segundo ∑C. Por tanto

RESTA

Puesto que la resta es un caso particular en la suma, es claro que:

NOTA: las expresiones                                                                 son diferentes.


La primera manda a incorporar la constante a cada dato de la variable antes de efectuar la sumatoria; la segunda, agrega la constante a la sumatoria; de los datos de la variable ejemplo:

 
4.- Sumatoria de una variable con un multiplicador o divisor constante.
La sumatoria de una variable con un multiplicador o un divisor constante es igual a la constante, en su función de multiplicador o divisor, por la sumatoria de los datos de la variable.
La expresión ∑CX ordena multiplicarla constante por cada dato dela variable X y luego hacer la sumatoria de los productos. Sustituyamos valores numéricos; ejemplo:

Veamos que los términos del segundo miembro tiene un factor constante. Por lo tanto:

El segundo miembro de esta igualdad es la constante que multiplica a los sumatorios delos datos de la variable de donde la 

Si la constante tiene una función de divisor, por un razonamiento análogo se muestra que:

También obsérvese en el primer miembro de la igualdad anterior ordena dividir cada dato de la variable entre la constante y luego sumar los cocientes; y el segundo, multiplicar el reciproco de la constante por la sumatoria de los datos de la variable, la expresión:
1/C         
También puede adoptar esta formula

5.-Sumatorias de potencias y raíces en una variable.
Para sumar potencias o raíces de una variable, primero se halla la potencia o la raíz y luego se lleva a cabo la sumatoria. Recordemos que un símbolo como  . Entonces: la expresión , indica elevar al cuadrado cada dato de la variable X y posteriormente sumar las potencias. Sustituyendo valores numéricos tenemos; ejemplo:

Estas operaciones son distintas a las que señala la expresión anterior 

en la cual se ejecuta primero la sumatoria y luego se eleva al cuadrado ejemplo:

Por lo cual es importante saber distinguir las expresiones. La primera la  

 representa la sumatoria de los cuadrados; la segunda 

, el cuadrado de la suma.
Y el caso de la sumatoria de las raíces de una variable por ejemplo:  

primero se extrae la raíz cuadrada o cada dato de la variable y luego se suman las raíces. Esto no es lo mismo que la expresión:  

6.- Regla para distribuir la sumatoria
Si después de la sumatoria encuentran entre paréntesis una expresión que incluye solo operaciones de suma o resta, la sumatoria puede ser distribuida entre los términos de la expresión. En símbolos:

Note que esta regla es valida para variables o constantes.


7.- Sumatoria de producto o el cociente de dos o más variables.
Si sumamos los productos de dos o más variables, algunos X y Y  tendremos la ∑XY.
Esta expresión manda a multiplicar cada dato de la variable y finalmente sumar los productos. Es decir:

Entonces: 

ejemplo:

 

NOTA: No confundir la ∑XY con ∑X(∑Y). Esta ultima se multiplica la sumatoria de los datos X por la sumatoria de los datos Y.

Necesitamos sumar el cociente dos variables, escribimos:
 Dividimos cada dato de la variable X entre el que le corresponde en la variable Y. esta expresión también es distinta a  , la cual indica el cociente de la sumatoria de los datos X entre la sumatoria de los datos Y.
EJERCICIOS: Con los datos siguientes efectúa las operaciones que se indican.